
Introduction to EEG and MEG
Below you will find a basic introduction into the most important aspects of EEG/MEG recording and analysis. If you are interested in this, why not look at our Imaging Wikis as well?
1. Introduction 6. Basic Differences Between EEG and MEG 7. Evoked and Induced Brain Responses
Basics of EEG and MEG: Physiology and data analysis
1. Introduction
The electrical activity of active nerve cells in the brain produces currents spreading through the head. These currents also reach the scalp surface, and resulting voltage differences on the scalp can be recorded as the electroencephalogram (EEG). The currents inside the head produce magnetic fields which can be measured above the scalp surface as the magnetoencephalogram (MEG). EEG and MEG reflect brain electrical activity with millisecond temporal resolution, and are the most direct correlate of on-line brain processing obtainable non-invasively. Unfortunately, the spatial resolution of these methods is limited for principal physical reasons. Even with an infinite amount of EEG and MEG recordings around the head, a non-ambiguous localisation of the activity inside the brain would not be possible. This "inverse problem" is comparable to reconstructing an object from its shadow: only some features (the shape) are uniquely determined, others have to be deduced on the ground of additional information. However, by imposing reasonable modelling constraints or by focussing on rough features of the activity distribution, useful inferences about the activity of interest can be made.
The continuous or spontaneous EEG (i.e. the signal which can be viewed directly during the recording) can be helpful in clinical environments, e.g. for diagnosing epilepsy or tumours, predicting epileptic seizures, detecting abnormal brain states or classifying sleep stages. The investigation of more specific perceptual or cognitive processes requires more sophisticated data processing, like averaging the signal over many trials. The resulting "event-related potentials" or "event-related magnetic fields" are characterised by a series of deflections or "components" in their time course, which are differentially pronounced at different recording sites on the head. They are classically labelled according to their polarity (positive/negative) at specific recording sites and the typical latency of their occurrence (e.g. N100 refers to a negative potential around 100ms, similarly for P300, N400 etc.). The amplitude and pattern of these components can be interpreted as dependent variables, which are distinguished by their dependency on the task, stimulus parameters, degree of attention etc.. Components related to basic perceptual processing (somato-sensory, visual, auditory, which are also termed "evoked potentials" or "evoked magnetic fields") can be used by clinicians to check the connection of the periphery to the cortex, or can assist in the diagnosis of brain death. Event-related potentials and magnetic fields are widely used to characterise the spatio-temporal pattern of brain activity in basically all areas of neuroscience. Latest developments include the combination of EEG/MEG with functional magnetic resonance imaging, for combining the superior spatial resolution of the latter with the better temporal resolution of the former.
2. Generation of the signals
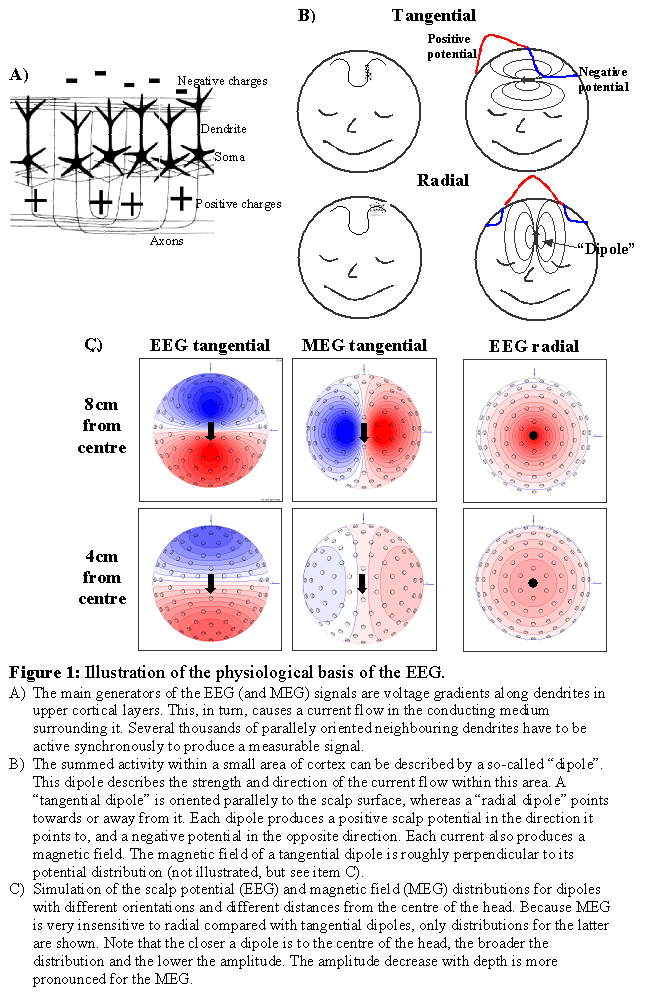
If an electrical signal is transmitted along an axon or dendrite, electrical charges are separated along very short distances on the corresponding cell membranes. Separated charges act as a small temporary "battery", with positive polarity at the side where the current is leaving and with negative polarity where the current is returning. These "batteries" are called "primary currents" since they are the sources of interest that reflect directly the activity of the corresponding neurons. The primary currents are embedded in a conductive medium, i.e. the brain tissue and brain liquor. Therefore a current is induced which flows through these media, as well as the skull and scalp, called "secondary" or "volume" currents. EEG would not be possible without volume currents, which also reach the scalp surface and cause voltage differences at the scalp that can be picked up by EEG electrodes. Both primary and volume currents produce magnetic fields, which sum up and can be measured by pick-up coils above the head using MEG.
Possible contributors to the measurable signals are: 1) Action potentials along the axons connecting neurons, 2) currents through the synaptic clefts connecting axons with neurons/dendrites, and 3) currents along dendrites from synapses to the soma of neurons. Action potentials are "quadrupolar", i.e. two opposing currents occur in vicinity of each other, the effects of which cancel each other out. In addition, action potentials last only a few milliseconds, making it more difficult to achieve a larger number of them being active simultaneously and to sum up to a measurable signal at larger distance. Synapses are very small and the current flow relatively slow. Furthermore, they can be located nearly randomly around a neuron and its dendrites, so that the contributions of different synapses are likely to cancel each other out. The current flow along post-synaptical dendrites is dipolar, and at least the apical dendrites in cortical pyramidal cells are generally parallely organised. They are typically active for about 10ms after synaptic input. For these reasons, the apical dendrites of the cortex are assumed to contribute strongest to the measurable EEG and MEG signals. Because this activity directly reflects processing of specific neurons, EEG and MEG are the most direct correlate of on-line brain processing obtainable non-invasively. However, one dendrite would be far too weak to produce a measurable signal, instead tens of thousands are required to be active synchronously. Consequently, EEG/MEG are only sensitive to coherent simultaneous activity of a large number of neurons. For modelling purposes it is important to note that many weak neighbouring dipolar sources can be summarised to one "dipole", which can be interpreted as a "piece of active cortex".
3. General data analysis
Sampling Recordings are taken virtually simultaneously at all recording sites at different time points. The time difference between sampling points is called the sampling interval. The sampling rate in Hertz (Hz) is given by the number of samples per second, i.e. (1000ms/{sampling interval in ms}). Typical sample intervals are of the order of several milliseconds, depending on the purpose of the study. If very short-lived brain processes are of interest, i.e. if the signal is to contain high frequency components, a higher sampling rate is required (for early somato-sensory or brain stem potentials, for example, a sampling rate of about 1000Hz or more is required). This, however, also means more data, i.e. more storage space is required and further processing will be slowed down. If slower brain processes are studied and only low frequency components are of interest, the sampling rate can be reduced (e.g. about 40Hz for slow waves like the readiness potential). In typical event-related potential or field studies, where the interesting frequencies usually lie between 0-100 Hz, a sampling rate of 200-500 Hz is common. With modern analysis equipment, the computing power and storage space is usually not a crucial issue any more.
Filtering If the signal of interest (e.g. a specific ERP component) is already roughly known, filters can be applied that suppress noise in frequency ranges where the signal has low amplitude. High-pass filters attenuate frequencies below a certain cut-off frequency (i.e. they "let pass" frequencies above it), while low-pass filters behave the other way round. A combination of a low-pass and a high-pass filter is called a band-pass filter. A typical band-pass filter for ERP studies would be 0.1-30Hz, but this highly depends on the signal of interest and the purpose of the study.
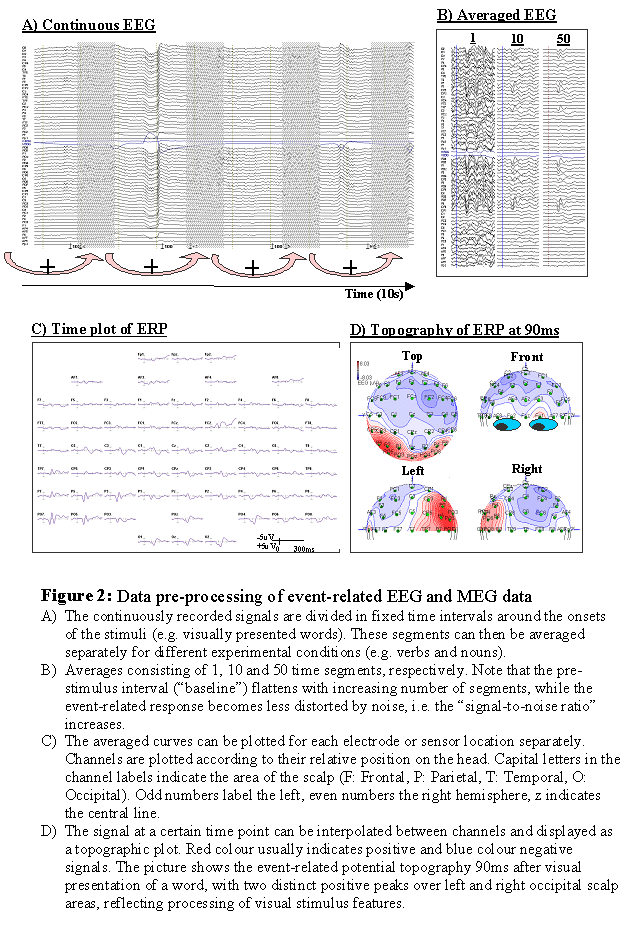
Averaging The brain response of a single event (i.e. the signal after the presentation of a single stimulus) is usually too weak to be detectable. The technique usually employed to cope with this problem is to average over many similar trials. The brain response following a certain stimulus in a certain task is assumed to be the same or at least very similar from trial to trial. That means the assumption is made that the brain response does not considerably change its timing or spatial distribution during the experiment. The data are therefore divided in time segments (or "bins") of a fixed length (e.g. one second) where the time point zero is defined as the onset of the stimulus, for example. These time segments can then be averaged together, either across all stimuli present in the study, or for sub-groups of stimuli that shall be compared to each other. Doing so, any random fluctuations will cancel each other out, since they might be positive in one segment, but negative in another. In contrast, any brain response time-locked to the presentation of the stimulus will add up constructively, and finally be visible in the average. The noise level is typically about 20uV, and the signal of interest about 5uV. If the noise was completely random, to reduce the amplitude of the noise by a factor of n one would have to average across n*n samples. Averaging over 100 segments would therefore reduce the noise level to about 2uV, at least less than half the amplitude of the signal of interest. A further 100 segments (i.e. 200 segments altogether) would reduce the noise level to about 1.4uV. To reduce the noise level achieved by 100 segments by a factor 2, one would need 400 segments (20uV/20=1uV), i.e. 4 times as many. The fact that the noise level in the average data decreases only with the square root of the number of trials poses a considerable limitation on the duration of an experiment, and should be carefully considered prior to setting up a study.
Baseline correction During the recording, EEG and MEG signals are undergoing slow shifts over time, such that the zero level might differ considerably across channels, though the smaller and faster signal fluctuation are similar. These signal shifts can be due to brain activity, but can also be caused by sweating (in the case of EEG), muscle tension, or other noise sources. It would therefore be desirable to have a time range where one can reasonably assume that the brain is not producing any stimulus related activity, and that any shift from the zero line is likely due to noise. In most ERP and ERF studies, this "baseline interval" is defined as several tens or hundreds of milliseconds preceding the stimulus. For each recording channel, the mean signal over this interval is computed, and subtracted from the signal at all time points. This procedure is usually referred to as "baseline correction". It is crucial in ERP and ERP experiments to ensure that an observed effect (e.g. an amplitude difference between the components evoked by two sorts of stimuli) is not already present in the signal before the stimuli were actually present. If this was the case, it would indicate that the signal is contaminated by a confound that is not stimulus-related.
Display In usual displays for time courses of EEG and MEG data, time is chosen as the x-axis and the amplitude as the y-axis. Traditionally, negative amplitudes are often (but not consistently) plotted upwards for EEG data. If multi-channel ERP and ERF recordings are presented, it is usual to project the recordings sites on a two-dimensional surface, and to plot the curves for these recording sites at the corresponding location. This gives a rough impression of the spatial distribution of the signal over time. However, with increasing number of recording channels, these images become very difficult to interpret. If the spatial distribution of a specific time point or time range (e.g. a peak) in the signal shall be analysed in more detail, the signal can be interpolated between recording sites and plotted as a colour-coded map. Often positive amplitudes are displayed in red colour, and negative amplitudes by blue colour.
4. EEG recordings
Referencing Electric potentials are only defined with respect to a reference, i.e. an arbitrarily chosen "zero level". The choice of the reference may differ depending on the purpose of the recording. This is similar to measures of height, where the zero level can be at sea level for the height of mountains, or at ground level for the height of a building, for example. For each EEG recording, a "reference electrode" has to be selected in advance. Ideally, this electrode would be affected by global voltage changes in the same manner as all the other electrodes, such that brain unspecific activity is subtracted out by the referencing (e.g. slow voltage shifts due to sweating). Also, the reference should not pick up signals which are not intended to be recorded, like heart activity, which would be "subtracted in" by the referencing. In most studies, a reference on the head but at some distance from the other recording electrodes is chosen. Such a reference can be the ear-lobes, the nose, or the mastoids (i.e. the bone behind the ears). With multi-channel recordings (e.g. >32 channels), it is common to compute the "average reference", i.e. to subtract the average over all electrodes from each electrodes for each time point. This distributes the "responsibility" over all electrodes, rather than assigning it to only one of them. If a single reference electrode was used during the recording, it is always possible to re-reference the data to any of the recording electrodes (or combinations of them, like their average) at a later stage of processing. In some cases "bipolar" recordings are carried out, where electrode pairs are applied and referenced against each other for each pair (e.g. left-right symmetrical electrodes).
Electrode locations To compare results over different studies, electrode locations must be standardised. These locations should be easily determinable for individual subjects. Common is the extended 10/20 system, where electrode locations are defined with respect to fractions of the distance between nasion-inion (front-back) and the pre-auricular points (left-right). Obviously, the relative locations of the electrodes with respect to specific brain structures can only be estimated very roughly. If this is a crucial point, electrode locations can be digitised together with some anatomical landmarks (like the pre-auricular points, the ear-holes, nasion or inion). These landmarks can also be detected in individual MRI or CT scans if available. The landmarks of the different co-ordinate systems (EEG digitisation, MRI/CT scan) can then be matched, such that both data sets are in the same co-ordinate system. Another possibility is to digitise a large number of points (at least several hundreds) evenly distributed over the scalp surface, and match those to the scalp surface segmented from the individual MRI/CT image. This makes possible more realistic modelling of the head geometry for sophisticated source estimation, and furthermore the visualisation of the results with respect to the individual brain geometry.
Fixation of electrodes Clinical recordings usually employ only few (1-9) electrodes at positions standardised for given purposes. Modern ERP studies that intend topographic analysis often employ 32 to 256 electrodes. If only a few electrodes are used, these can be glued to the skin by hand, using electrically conducting glue. With larger numbers of electrodes, electrodes are commonly mounted on a cap. Contact with the skin has then to be made by introducing a electrically conducting substance between skin and electrode. Depending on the device, this can be conducting gel, glue, or sponges soaked with a saline solution. For special applications, needle electrodes (subduran) are used. Electrodes can be of different materials: Tin electrodes are cheap but not recommended at low frequencies. Ag/AgCl (silver-silver-chloride) electrodes are suitable for a larger frequency range and most commonly used in research. Gold and platin electrodes are used for special requirements. The amplitude of the raw signal that is recorded is of the order of 50 uV, i.e. about a million times weaker than those by household batteries. It therefore required special amplifiers that amplify the signal and convert it to a digital signal that can be stored and processed on a computer. This has to be accomplished at high sampling rates (several hundred or thousand recordings a second), and virtually simultaneously for each recording channel.
5. MEG recordings
SQUIDS The amplitude of the magnetic fields produced spontaneously by the human brain are of the order piko-Tesla when recorded, and that of the evoked responses is around 100fT (i.e. more than one million times smaller than the earth's magnetic field). These very low field strenghts can be recorded by so-called "Superconducting Interference Devices" (SQUIDS): A specially prepared pick-up coil is cooled down to superconductivity by liquid helium, and exploiting a specific quantum effect the magnetic flux through the coil is measured.
Influence of coil types The magnetic field, in contrast to the electric potential, has a direction, usually illustrated by magnetic field lines. A current flowing along a straight line produces circular magnetic field lines that are concentric with respect to the current line. If the thumb of your right hand points in the direction of the current flow (which is from negative to positive polarity, or "from minus to plus"), then the remaining fingers point in the direction of the magnetic field ('right-hand-rule'). The coils pick up only the strength of the magnetic field in the direction perpendicular to the coil area. Different coil configurations are in use: A single coil is called a 'magnetometer'. If the difference between two or more neighbouring coils is measured, it is called a (first order, second order etc.) 'gradiometer'. Gradiometers have the property to be less sensitive to sources at larger distances, because those have more similar field strengths at all coils, which in the difference yields lower values. This has the advantage that noise sources at larger distances are also suppressed (like the heart, or electric devices near the recording system). Because MEG sensors are so very sensitive, they have to be well-shielded against magnetic noise. The shielding of the laboratory and the SQUID technology make an MEG device 10 to 100 times more expensive than an EEG system, and the permanent helium-cooling imposes considerable maintenance costs.
Insensitivity to radial and deep sources A special and important feature of MEG is its insensitivity to current sources which are "radial", i.e. which are directed towards or away from the scalp (like the top of a cortical gyrus). It mainly "sees" tangential sources, which are parallel to the scalp. The full explanation for this characteristic would involve a fair amount of physics and mathematics, but an idea can given for the following simplified situation. Imagine the head was modelled as a sphere, and the recording coil would be tangentially placed above its surface. A dipole within the sphere pointing towards the coil would produce a magnetic field parallel to the coil, which would therefore not be measured. The volume currents, on the other side, are symmetric with respect to the axis along the dipole direction. This means that the magnetic field through the coil by the current on one side of this axis is cancelled by the current on the other side. Therefore the contribution of the primary current as well as that of the volume current vanish. More detailed analysis of this problem shows that the magnetic field of a radial dipole in a spherical volume conductor generally vanishes at all possible recording sites. A special case of a radial dipole is a dipole located at the centre of the sphere: It must necessarily point away from the centre, and is therefore radial and "invisible" for MEG. Roughly speaking, the nearer a source is to the centre, "the more radial" it is. This implies that the deeper a source, the less visible it is for MEG. This seems to be a disadvantage for the MEG, but turns into an advantage if superficial and tangential sources are targeted at, since in that case the corresponding MEG signal is less contaminated by other disturbing sources.
6. Basic differences between EEG and MEG
Both EEG and MEG are sensitive to the topography of the brain – the details of the structure of its surface. The brain surface is quite dramatically folded, and whether the signal arises in the convex tops of the folds (gyri) or the concave depths of the folds (sulci) affects sensitivity to neuronal current sources (dipoles). MEG is particularly insensitive to radial dipoles, those directed towards or away from the scalp (like at the top of a gyrus). It mainly 'sees' tangential dipoles, which are parallel to the scalp. The reason for this is that if the head were a perfect sphere (a reasonable first approximation for an average head shape), all magnetic fields resulting from a radial dipole (including the volume currents) cancel each other out at the surface (a more detailed explanation would involve a fair amounts of physics). EEG is sensitive to both radial and tangential dipoles.
A special case of a radial dipole is a dipole located at the centre of a sphere: it must necessarily point away from the centre, and is therefore radial and 'invisible' for MEG. Roughly speaking, the nearer a source is to the centre, 'the more radial' it is. This implies that the deeper a source is in the head, the less visible it is for MEG. This seems to be a disadvantage for MEG, but turns into an advantage if superficial and tangential sources (e.g. in sulci of the cortex) are targeted, since in that case the corresponding MEG signal is less contaminated than EEG by other possibly disturbing sources. Furthermore, it has been shown that superficial and tangential sources can be localized with more accuracy than with EEG, particular in somatosensory and some auditory parts of the brain. MEG has therefore been widely used to study early acoustic and phonetic processing, and the plasticity of the somatosensory and auditory system.
The basics of EEG were invented in the 1920s, mainly with medical applications in mind. EEG is widely used in clinical diagnostics and research. The first MEG systems (starting with 1-channel!) appeared in the late 1960s, and first commercial systems took off in the 1980. The development was mainly driven by engineers and physicists. This, and possibly the fact that MEG is much more expensive than EEG, often makes these two look like very different methods with very different applications. It is important to keep in mind, however, that both techniques measure the same type of brain activity from slightly different angles. As a general rule, EEG "sees more" of the brain, but is less able to localise this activity. MEG "sees less" of the brain, but what it sees it can localise better. As we will see below, a combination of EEG and MEG is superior for localisation than each method on its own. If localisation is not the main focus of a study, EEG may often be sufficient, for example in many clinical environments.
7. Evoked and Induced Brain Responses
The averaging procedure described above assumes that there is something like the average brain response, i.e. a signal with roughly the same time course in every epoch for a particular stimulus category. But what if the timing changes slightly from epoch to epoch? If this jitter across epochs is small compared to the time-scale of the signal, one does not have to worry. But what if the signal consists of a rapid sequence of positive and negative deflections (e.g. an "oscillation")? Then the jitter may sometimes result in a positive value in some epochs, and negative values in other epochs. Across epochs, this may average out to zero. This could be the case with co-called "gamma oscillations" – a signal in the frequency range above 30 Hz (definitions differ slightly), which has been associated with complex stimulus processing such as Gestalt perception. These gamma oscillations may occur time-locked to a stimulus (e.g. always between 200 and 300 ms after picture onset). However, the "phase information", i.e. the exact occurrence in time of maxima and minima of the oscillations, may vary across epochs. These signals are called "induced", or order to distinguish them from the above-mentioned "evoked" signals that are both time- and phase-locked to the stimulus. In order to extract induced signals from the data, the frequency power spectrum (i.e. the signal amplitude for different frequency bands) has to be computed for every epoch separately. The power spectrum only contains information about the amplitude of the signal for a certain frequency in a certain latency range, but no phase information. If there are consistent gamma oscillations between 200 and 300 ms after every picture, the spectral power in the gamma frequency range should be consistently above baseline level in the latency range across epochs. This method has been applied to studies on Gestalt perception, as illustrated in the figure below. For example, it has been found that gamma band activity is usually larger when an incomplete but meaningful pattern is perceived, compared to either non-meaningful or easily recognisable patterns.

8. Statistical analysis
The statistical analysis of EEG/MEG data is as yet not fully standardised, and the strategies employed can vary considerably depending on the hypothesis and purpose underlying the experiment. The most frequent approach is the "Analysis of Variance" or "ANOVA". The signal amplitudes for different electrodes, sensors or dipoles are considered as dependent variables, and extracted for each subject (e.g. like mean reaction times or error rates per subject in behavioural experiments). Imagine a so-called oddball experiment, in which subjects are presented with two different tones: One tone of 600Hz, which occurs 90% of the time, and another tone of 1000Hz, which occurs only 10% of the time. Subjects are required to press different buttons in response to the frequent and rare tones. Does the maximum amplitude of the ERP in a certain time range change as a function of the probability of the tone? In this case, one would first have to decide which time range to analyse. In this kind of oddball experiment, it is known that rare tones produce a so-called "P300", i.e. a positive deflection of the ERP around centro-parietal electrode sites, which usually reaches its maximum around 300ms after stimulus onset. It would therefore be reasonable to look for the largest peak around 300ms at the electrode Pz, and to extract the amplitudes at this electrode and this point in time for all subjects. These values would enter the ANOVA as a dependent variable. "Probability" would be a single, two-level factor allowing for a comparison between values obtained for the presentation of the rare tones with those obtained for the frequent tones. In general, the result is that the amplitude of the P300 is larger for rare tones. Does only the amplitude change with the toneâs probability of occurrence, or could there also be a change of "Laterality"? In other words, could the rare tones produce larger amplitudes in either the left or right hemisphere compared with the frequent ones? In this case, one would have to extract amplitude values for at least two electrodes, one in the left and one in the right hemisphere (e.g. P5 and P6, left and right of Pz). The ANOVA now has two factors: Probability (rare and frequent) and Laterality (left and right). If the laterality changes with tone probability, one should obtain an interaction between Probability and Laterality. In the case of simple tones, such an interaction is generally not found, although it might be expected for more complex (e.g. language-related) stimuli. If such a hypothesis-based approach is not suitable (e.g. because there is no specific hypothesis, or because the hypothesis was falsified but one still does not want to give up...), exploratory strategies have to be used. For example, separate statistical tests (like paired T-tests) can be computed electrode by electrode, or dipole by dipole. However, if we perform statistical comparisons at different recording sites or source locations, and each of those by itself has a chance of 5% to produce a false positive (i.e. tells us there is a significant difference when in fact there is not), then we have to expect that a fraction of 5% of our locations are incorrectly labeled as significant. This is the common problem of multiple comparisons. Methods to deal with this problem in the case of EEG and MEG data are currently under development.
9. Estimating the neuronal sources
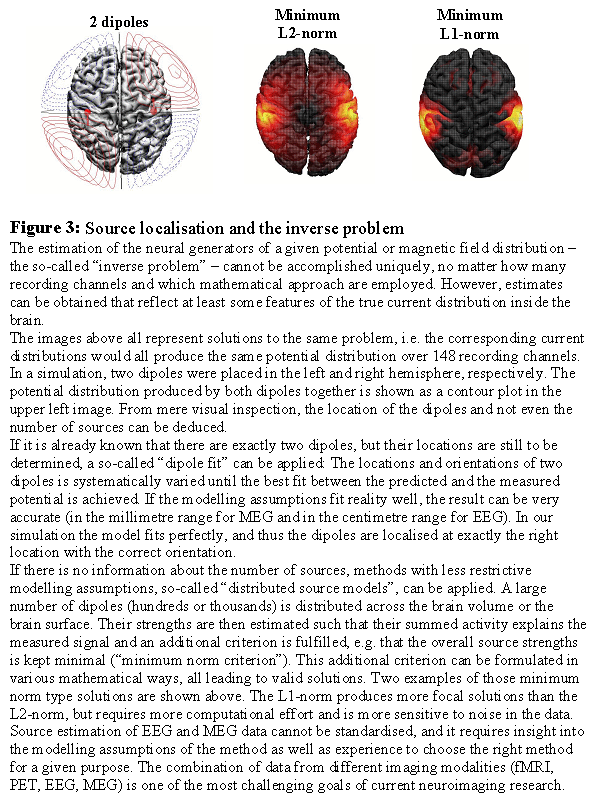
Underdeterminacy of the inverse problem Even if the EEG and MEG were measured simultaneously at infinitely many points around the head, the information would still be insufficient to uniquely compute the distribution of currents within the brain that generated these signals. The so-called "inverse problem", i.e. the estimation of the sources given the measured signals, is "under-determined" or "ill-posed". But all is not lost: By imposing appropriate modelling constraints, one can often derive valuable information about spatial features of the source distribution from the data. The main questions in this context are: Do I have enough information from other sources (neuropsychology, other neuro-imaging results) to narrow down the possible generators? Or can I ask my questions such that it is not necessary to know the exact source distribution, but only some rough features that can be determined without further modelling constraints?
Approaches to deal with the inverse problem One can distinguish between two strategies to tackle the inverse problem: 1) Approaches that make specific modelling assumptions, like the number of focal sources needed to produce the recorded data and their approximate location, and 2) approaches that make as little modelling assumptions as possible, and focus on rough features of the current distribution that are determined by the data rather than specific modelling assumptions (like laterality). Under 1) fall the so-called 'dipole models': The number of active dipoles, i.e. small pieces of activated cortex, is assumed to be known (usually only a few). An initial guess about their location and orientation is made, and these parameters are then adjusted step by step until the predicted electric potential or magnetic field resembles the measured one within certain limits. These methods have been successfully applied in studies of perceptual processes and early evoked components. Point 2) comprises the 'distributed source models': The naturally continuous real source distribution is approximated by a large number (several hundreds or thousands) of sources equally distributed over the brain. The strengths of all these sources cannot be estimated independently of each other, but at least a "blurred" version of the real source distribution can often be obtained. Peaks in this estimated current distribution might correspond to centres of activity in the real current distribution. These methods are preferred if modelling assumptions for dipole models cannot be justified, like in cognitive tasks or in noisy data.
10. EEG, MEG and fMRI: Localisation Issues
Although the signals of EEG and MEG are generated by the same sources (electrical currents in the brain), they are both sensitive to different aspects of these sources (as described above). This could be compared to viewing the shadows of the same object from two different angles. It should not be surprising then that the information of EEG and MEG are complementary, and combining the two in source estimation usually yields more accurate result than using either method alone. However, this also means more work, and not everybody has both EEG and MEG available. It is therefore important to decide at the beginning of a study 1) whether localisation is required at all; 2) whether absolute anatomical localisation is required (e.g. in combination with structural MRI images), or whether relative localisation (e.g. "left more than right") is sufficient; 3) whether it is already known that the sources are visible in EEG, MEG or both.
While for EEG and MEG, we can safely assume that we are measuring the same sources from different angles, the same cannot be said for fMRI compared to EEG/MEG. Standard fMRI measures a blood-oxygen-level dependent (BOLD) signal. This is a metabolic (rather than electric) signal, depending on how much oxygen is consumed in different brain areas. Its time course after stimulus presentation usually peaks around 5 s, but can last for up to 30 s. This is a much slower time scale than the millisecond temporal resolution of EEG and MEG. fMRI data are therefore usually not presented over time, but as one image that collapses brain activation over several seconds. There is still no clear model of how the electrophysiological sources of EEG and MEG relate to the metabolical fMRI signal. It cannot be generally assumed that activation hot spots in fMRI are also visible in EEG/MEG, or vice versa. Even if there is some correspondence, brain areas shown as activated in fMRI maps may activate at different time points in EEG/MEG. So far, some successful combinations of EEG/MEG with fMRI have been achieved for relatively simple perceptual processes. These are usually reflected in early EEG/MEG signals, and can be localised to a few focal brain areas.
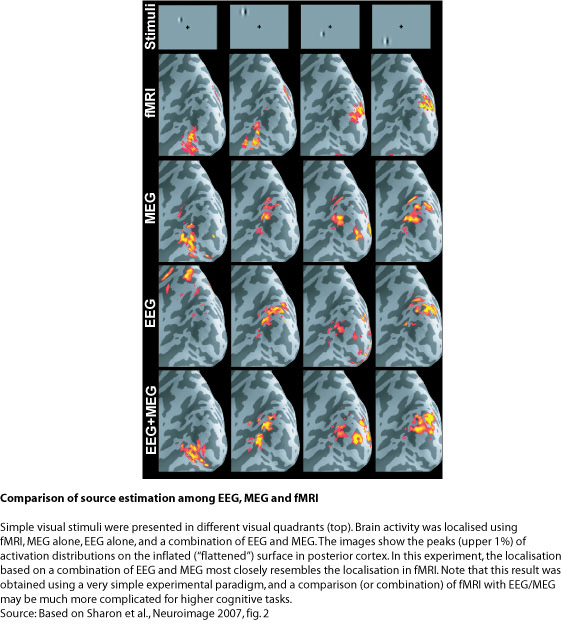
In the example presented in the figure below, the combination of EEG and MEG for the estimation of early visually evoked responses is compared to fMRI data. Simple visual stimuli (socalled Gabor patches) were flashed in the four quadrants of the visual field (upper left, upper right, lower left, lower right). It is known that such stimuli activate characteristic retinotopic areas of limited extent (~ 1 cm2) in visual cortex in the occipital lobe (cortical area V1). Changing the stimulus location therefore changes the cortical response location in a predictable way. For example, visual stimuli presented in the left visual hemifield activate V1 in the right cortical hemisphere, and vice versa for right hemifield stimuli. Similarly, stimuli in the upper/lower visual field activate lower/upper parts of V1. This response pattern can then be compared across different localisation techniques.
The expected pattern of activation is clearly present in the fMRI data presented at the top of the figure below. This technique provides millimetre spatial resolution, but does not tell us whether this activation reflects early or late processes. EEG and MEG show a similar pattern around 74 ms after stimulus onset – this is about the time when visual information from the retina first reaches visual cortex. Localisations for EEG and MEG separately show approximately the same patterns, although EEG alone is quite far off in one case (left panel). The combination of EEG and MEG, however, nicely resembles the pattern obtained using fMRI. It confirms that this pattern reflects an early processing stage in visual cortex.
Note that the images for fMRI as well EEG/MEG are "tresholded", i.e. only activations above a certain value are shown. These represent the "tip of the iceberg", but the true spatial extent of activation can be difficult to determine. Especially for the case of EEG/MEG one has to keep in mind that spatial resolution is fundamentally limited, and that the estimated activations are always more blurred than the true underlying neural sources. Furthermore, there is no perfect match between fMRI and EEG/MEG. It is not clear whether this reflects the resolution limits of these methods, or fundamentally different physiological sources of the signals (electrical vs. metabolic). For this simple data set, the correspondence between the imaging techniques appears to be very high. However, for higher cognitive processes, the discrepancy may be much larger. A combination of these two imaging modalities should be considered with great care - an independent analysis and later comparison of fMRI and EEG/MEG may be more appropriate.
Any feedback and suggestions welcome!
Olaf Hauk
