Dealing with difference
Forgive this stub page, but...
Hemodynamic responses can differ from brain area to brain area. Of course neuronal response shapes can also differ. In either case, convolving your event onset with the canonical SPM HRF will give you a model that may be correct for some areas but not others. One classic citation on this is:
@article{aguirre1997eab,
title={{Empirical Analyses of BOLD fMRI Statistics}},
author={Aguirre, GK and Zarahn, E. and D'Esposito, M.},
journal={Neuroimage},
volume={5},
number={3},
pages={199--212},
year={1997},
publisher={Elsevier}
}Another problem that can occur with using the canonical HRF is when there are residual timing differences between slices - for example when you have not used some slice-time correction before statistics.
Using the temporal derivative
One standard way to deal with this is to add the HRF temporal derivative (TD) to your basis functions, along with the canonical HRF. You can also add the spatial derivative (SD). This creates further complexity for your second level analysis. Approaches are:
Dealing with the temporal derivative at the second level
- Ignore the TD at the second level, using only HRF contrasts. The TD, for short-event designs, will be more or less orthogonal to the HRF, so in this case your second level analysis will be more or less identical to the same analysis without using the TDs at the first level. Be careful using the TD for longer events or blocks, because in this case you may find the TD is not orthogonal to the HRF, and the analyses will differ, and, in particular, you may lose power in your HRF second level analysis.
- Do an F test at the second level using the HRF and TD as the two effects you want to model at the second level. Note that the HRF and TD will probably be correlated within subject, so you will need to adjust for this in your SPM variance modeling. This looks for variance explained by the HRF and TD. Therefore, if your TD does not explain variance, you will lose power compared to looking only at the HRF.
- Do an adjustment that takes into account the HRF and TD together, looking only for the case where there is a plausible HRF and TD.
The following sections are about approaches to this problem.
Calhoun approach to combining the HRF and TD
@article{worsley2006dfa,
title={{Detecting fMRI activation allowing for unknown latency of the hemodynamic response}},
author={Worsley, KJ and Taylor, JE},
journal={Neuroimage},
volume={29},
number={2},
pages={649--654},
year={2006},
publisher={Elsevier}
}This paper suggests taking HRF and TD, and doing the following transformation (matlab syntax):
combined = sign(HRF) .* sqrt(HRF.^2 + TD.^2)
This will have the effect of looking at the combination of the two, with the up-downness from the HRF only. Several papers have used this. The caveat is that this transform, on the null hypothesis, does not generate a normal distribution. Here's a plot from lots of pairs of random numbers combined in this way:
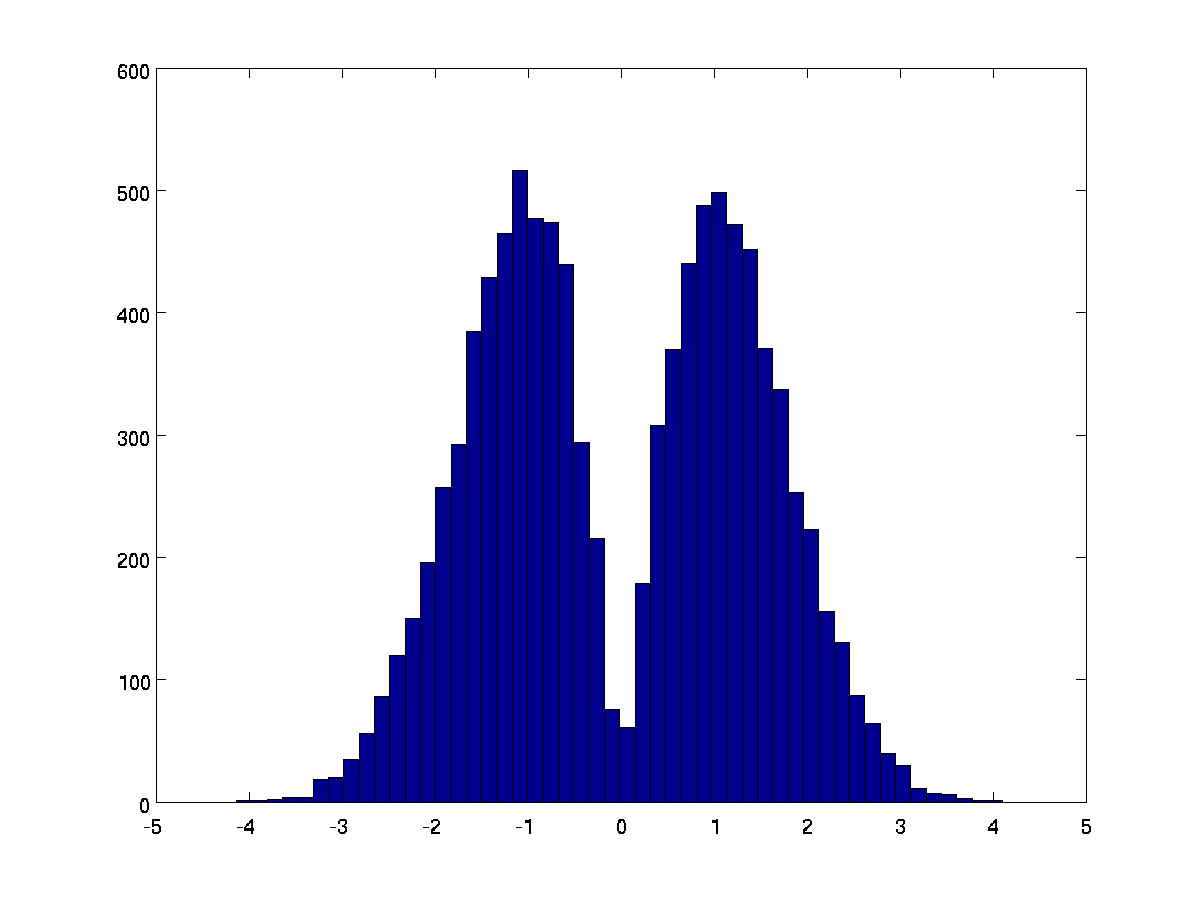
In practice, software to apply this transform usually only applies it to a subset of voxels - for example where the ratio of HRF to TD is greater than 1 - otherwise you use the HRF only. This means that the data to which the transform _is_ applied will be as above, and data to which it is not applied will be the same as the HRF. We can also do spatial smoothing of the difference between the HRF alone and the HRF+TD transform, to regularize it a bit in space.
Taylor + Worsley approach
@article{worsley2006dfa,
title={{Detecting fMRI activation allowing for unknown latency of the hemodynamic response}},
author={Worsley, KJ and Taylor, JE},
journal={Neuroimage},
volume={29},
number={2},
pages={649--654},
year={2006},
publisher={Elsevier}
}
@article{taylor2006ima,
title={{Inference for magnitudes and delays of responses in the FIAC data using BRAINSTAT/FMRISTAT}},
author={Taylor, JE and Worsley, KJ},
journal={Human Brain Mapping},
volume={27},
number={5},
pages={434--441},
year={2006},
pdf={http://www.math.mcgill.ca/keith/fiac/fiac.pdf}
}